More complex combinational logic#
The two-input, single-output \(\tt AND\), \(\tt OR\), and \(\tt NOT\) operations we have looked at so far are the simplest logic functions. There are three ways that we can increase in complexity:
Using other basic logic functions
Increasing the number of inputs
Increasing both the number of inputs and the number of outputs
This chapter investigates each in turn.
Other basic logic functions#
XOR#
We can write this in shorthand as
\[
X = A\ {\tt XOR}\ B
\]
or
\[
X = A \oplus B
\]
\(A\) |
\(B\) |
\(X\) |
|---|---|---|
0 |
0 |
0 |
0 |
1 |
1 |
1 |
0 |
1 |
1 |
1 |
0 |
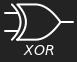
Fig. 3 \(\tt XOR\) function as circuit element.#
NOR#
We can write this in shorthand as
\[
X = A\ {\tt NOR}\ B
\]
or
\[
X = \overline{A + B}
\]
\(A\) |
\(B\) |
\(X\) |
|---|---|---|
0 |
0 |
1 |
0 |
1 |
0 |
1 |
0 |
0 |
1 |
1 |
0 |
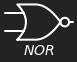
Fig. 4 \(\tt NOR\) function as circuit element.#
NAND#
We can write this in shorthand as
\[
X = A\ {\tt NAND}\ B
\]
or
\[
X = \overline{AB}
\]
\(A\) |
\(B\) |
\(X\) |
|---|---|---|
0 |
0 |
1 |
0 |
1 |
1 |
1 |
0 |
1 |
1 |
1 |
0 |
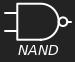
Fig. 5 \(\tt NAND\) function as circuit element.#
