Amplitude Modulation

Amplitude modulation modifies equation (1)

\[ s(t) = A(t) \cos\big(\omega(t) t + \phi(t)\big) \]

and sets

\[\begin{split} \begin{align*} A(t) &= A_{\tt offset} + \beta_{A} m(t) \\ \omega(t)t &= \omega_c \\ \phi(t) &= \phi_c \end{align*} \end{split}\]

where

\(A_{\tt offset} \) is the amplitude offset,
\(\beta_A\) is the amplitude deviation, assuming \( \left | m(t) \right | \le 1\)
\(\omega_c\) is the constant center frequency,
\(\phi_c\) is the constant phase.

so that

(3)\[ s(t) = (A_{\tt offset} + \beta_{A} m(t)) \cos\left(\omega_c t + \phi_c\right) \]

Below are two examples of amplitude modulated signals where the message, \(m(t)\) is a sine wave.

The first example sets \(A_{\tt offset} = 0\) while the second sets \(A_{\tt offset} = 1\).

When \(A_{\tt offset} = 0\) there is no energy at the carrier frequency. This mode of amplitude modulation is sometimes called suppressed carrier.

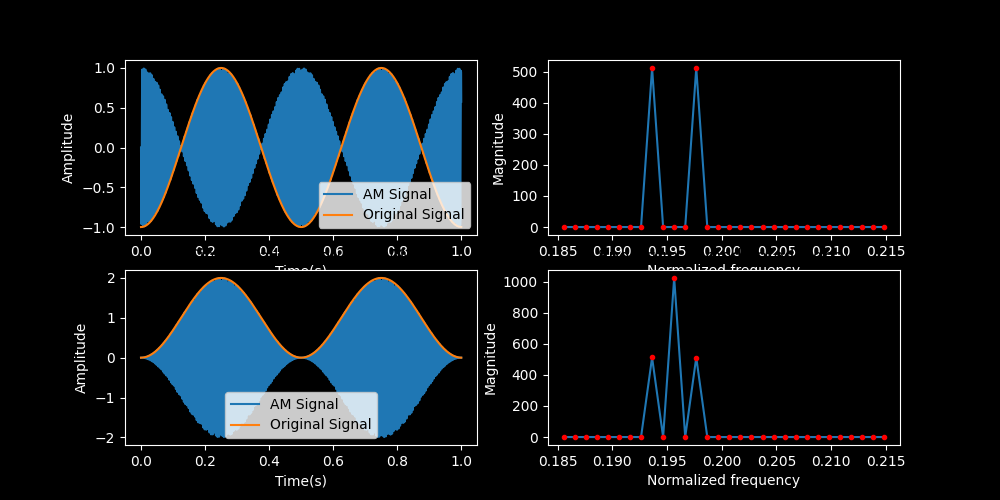
Fig. 1 The plots show the time-domain version of a sinusoidally modulated AM signal and the positive frequency spectrum of the signal (zoomed into the peaks).