Frequency Modulation

Frequency modulation takes the signal (1)

\[ s(t) = A(t) \cos\big(\omega(t) t + \phi(t)\big) \]

and sets

\[\begin{split} \begin{align*} A(t) &= A_c\\ \omega(t)t &= \int_0^t \omega_c + \beta_\omega m(t) dt \\ &= \omega_c t + \beta_\omega \int_0^t m(t) dt \\ \phi(t) &= \phi_c \end{align*} \end{split}\]

where

\(A_c\) is the constant amplitude,
\(\omega_c\) is the constant center frequency,
\(\beta_\omega\) is the frequency deviation, assuming \( \left | \displaystyle\int_0^t m(t) dt \right | \le 1\)
\(\phi_c\) is the constant phase.

so that

(4)\[ s(t) = A_c \cos\left(\omega_c t + \beta_\omega \int_0^t m(t) dt + \phi_c\right) \]

Below is an example of a frequency modulated signal where the message, \(m(t)\) is a sine wave.

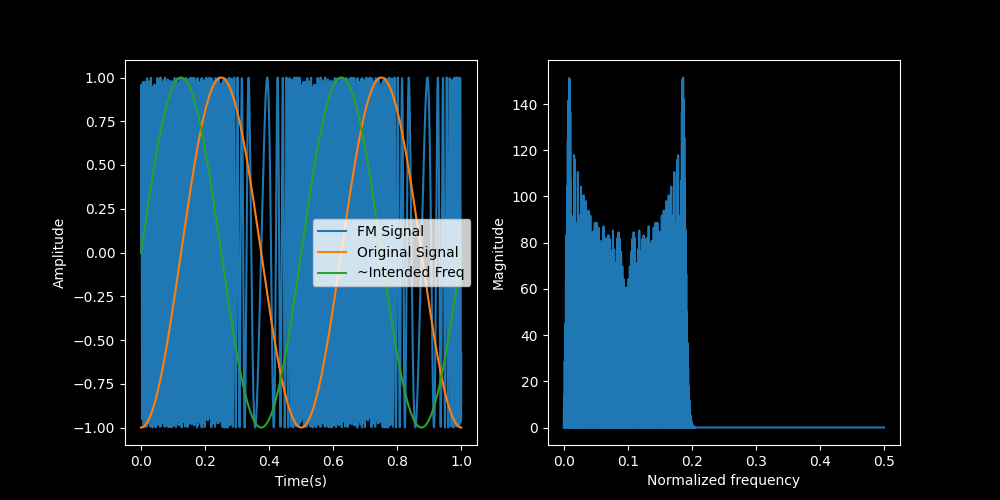
Fig. 2 The plots show the time-domain version of a sinusoidally modulated FM signal and the positive frequency spectrum of the signal.